Myth, Magic and Mathematics

Using only three simple tools – String, Straight-edge and Shadow – humans revealed the basic principles and constructions of elementary geometry. In this fascinating extract, Julia E. Diggins imagines how Pythagoras might have taught his famous theorem:

Listen to our baffling problem. Here is the Egyptian right triangle, the one used by the rope-stretchers, where the sides of the right angle are 3 units and 4 units, and the hypotenuse is 5 units.” Pythagoras drew it on a sandy space and then added a square on each side, and inner squares.

“There! You can see, by counting or by calculating the square units, that the total area of the squares on the two sides of the right angle is equal to the area of the square on the hypotenuse.”
He beckoned to the newcomers, who crowded close, multiplying and counting at the same time until all their heads nodded in agreement.

(3 × 3) + (4 × 4) = (5 × 5)
9 + 16 = 25

“Now let me show you a Greek design involving right triangles.” He drew their attention to the tiled floor on which they were standing, and then traced a similar pattern on the sand, outlining the important parts.

“Here the two sides of the right angle are equal, and the same relation holds.” With his pointer, he indicated one triangle and the related squares, and they all counted together.

“Look! Two triangles plus two triangles equals four triangles. The total area of the squares on the two sides of this right triangle is likewise equal to the area of the square on its hypotenuse.”
Again he waited until the newcomers nodded their assent, and then continued:

“In India the priests know other constructions that give similar results; they guard these numbers closely, but we have found some of them. In Babylon, a priestly astrologer whispered to me that there was a secret about this mystery that had never been penetrated.”

Now the attention was almost breathless as Pythagoras intoned solemnly: “That secret is our problem! Would the same relation always be true of any right triangle, no matter what the length of its sides, and how could you show this?”

At this dramatic moment, he withdrew behind a curtain, while attendants played on stringed instruments to indicate an intermission. Pandemonium broke out among the assembled initiates. All the newcomers began talking at once, making suggestions, arguing and shouting. The older mathematicians, who had worked on the problem themselves, were less noisy but even more excited. Finally Pythagoras reappeared. Silence instantly fell over the group as he resumed his lecture.

“I will now show you how to construct a wondrous figure which discloses that the answer is always yes! Today I will just draw it quickly, so you can all see my great discovery.”

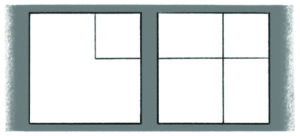He signalled to attendants to smooth the sand, and began to draw, using his pointer to emphasise his words.

“Watch this beautiful construction! I make a square frame, any size, and in its corner I place a small square, any size. Next I draw straight lines, continuing the sides of the small square to the edge of the frame.

“Do you see what my frame now contains? A small square and a medium square, and two equal rectangles.

“And next – we are almost there – I simply add diagonal lines across the rectangles!

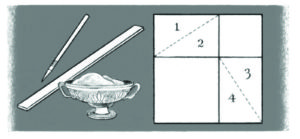“This is the figure I need. My frame now contains a small square, a medium square and four equal right triangles. Now I will ask you to look more closely at this figure.”

Pythagoras beckoned to the attendants, who poured coloured sand from jars onto the parts of the drawing, so the pattern showed plainly.

“Look again!” He used his pointer and spoke with care. “All the triangles, you know, are equal; each is the same triangle in a different position. Now, notice how the triangles touch the squares, especially Triangle 2.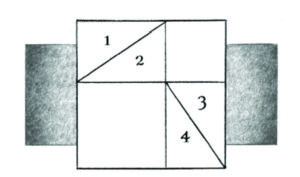 You can see that the small square is the square on the short side of the triangle. And the medium square is the square on the long side of the triangle. So my frame is completely filled by four equal right triangles plus the square on the short side and the square on the long side!”

Pythagoras paused while a low murmur of awe rose from the initiates.

“Now watch!” he intoned. And while they all craned their necks to see and the attendants poured more coloured sand, Pythagoras drew his final masterful figure.

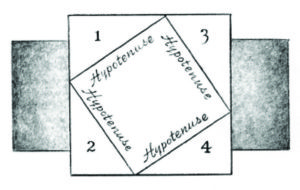“Watch well! I have only to swing and push these four triangles around, like this, so that they fit perfectly into the four corners of the frame, and my frame is now completely filled by the same four equal right triangles plus the square on the hypotenuse!

“Therefore, in any right triangle, the area of the square on one side plus the area of the square on the other side will add up to the area of the square on the hypotenuse!”

A mighty shout – we can imagine – went up from the assembled group. For this theorem was a true landmark in the development of geometry by the Pythagoreans. Almost all later geometric work involving lengths and measurement was based upon it. And this style of solving problems, especially equations, by diagramming them, would remain a chief trait of Greek geometry.

About the Book

“Whether you are learning geometry for the first time, teaching it to students at home or in the classroom, or are parents helping your children through their first geometry course, this is a must-read for everyone! You will be fascinated with the graphic illustrations and written depiction of how the knowledge and wisdom of so many cultures helped shape our civilization today.”
– Waldorf Books

String, Straight-edge and Shadow weaves history and legend to explain the story of geometry and the discoveries of the most famous mathematicians. A useful and inspiring book for those teaching geometry.

Check out our Steiner-Waldorf Teachers’ Hub for information on relevant books, downloadable resources and FAQs.